|
基于時頻域的鋼桶泄漏檢測信號處理(3)
范佩西
第三章 泄漏聲發射信號的時頻分析
本文是利用MATLAB軟件對鋼桶聲發射信號進行仿真時頻分析處理。根據采集到的鋼桶聲發射數據設波形的采樣頻率fs為1000kHz,采樣點數N為2048個,則時間t=n/fs,n為2048個點中的任意一點,n=0:N-1。分別在聲發射信號的時域和頻域對信號進行分析。
3.1 泄漏信號的頻域分析
鋼桶泄漏聲發射信號具有很寬的頻譜,它不僅包括可聽聲波范圍內的頻率成分,而且還包括超聲頻段內的頻率成分。這些頻率成分的信號和噪聲都可能沿著泄漏鋼桶傳播到傳感器,所以傳感器采集到的泄漏信號的頻譜有比較豐富的成分[1]。如圖3.2所示,有一定的泄漏信號存在于從0-150KHz頻率范圍內。而我們需要的對鋼桶泄漏檢測有用聲發射信號的只是某一頻段的信號,其他的不是我們所需要的,而且還對檢測信號有影響,所以我們必須對采集到的聲發射信號進行處理,需要除掉沒有的部分,留下我們需要的部分。
3.1.1 頻譜分析
傅里葉變換是一種分析信號的方法[2],它可分析信號的成分,也可用這些成分合成信號[2]。MATLAB中提供了多種實現快速變換的函數,如fft,ifft,fft2,ifft2等函數。其中fft2、ifft2是對離散數據分別進行二維快速傅里葉正、反變換。fft、ifft則是對離散數據分別進行一維快速傅里葉正、反變換[2]。由于MATLAB中沒有零下標,因此,它采用的公式上、下標都相應右移一位。
下面對實驗采集到的鋼桶聲發射信號做FFT,程序代碼如圖3.1所示。

圖3.1 FFT部分程序代碼
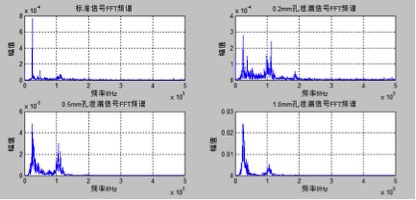
圖3.2 鋼桶聲發射信號的頻譜圖
經FFT得出如圖3.2所示的波形。比較泄漏信號與標準信號的FFT,泄漏信號在110KHz附近的幅度明顯比標準信號的大。比較不同泄漏孔徑大小的泄漏信號,110KHz附近的幅度隨孔徑的增大而增大。所以泄漏聲發射信號的特征頻率明顯是在110kHz附近,而25kHz附近的為噪聲頻率。
3.1.2 泄漏聲發射信號的降噪處理
鋼桶泄漏聲發射信號經過鋼桶壁、傳感器、信號采集卡、傳輸設備、放大器等會使信號伴隨有很多噪聲,這些噪聲的大量參入使鋼桶泄漏源的聲發射信號發生改變,從而會使鋼桶泄漏檢測的精確性和準確度降低,所以我們必須尋找一定的信號處理方法來降低噪聲,是真正的泄漏聲發射信號強度增大。
由以上FFT得到的頻譜圖可知,鋼桶泄漏聲發射信號在頻域內有兩處比較明顯的突起,一個為噪聲,一個為聲發射信號特征頻率。因為鋼桶聲發射特征頻率在110kHz附近,我們需要濾掉高頻和低頻的信號,又因為鋼桶泄漏聲發射信號是一類非平穩的隨機信號,所以應該選擇一種適合非平穩的隨機信號的濾波方法——FIR帶通濾波[26]。

圖3.3 FIR濾波器界面
文中主要采用MATLAB工具FDATool的設計FIR濾波器,如圖3.3所示。可以有效的實現對聲發射信號的濾波。基于鋼桶泄漏聲發射信號特征和FIR濾波器各具體參數要求[23],初步設計得到濾波器幅值—頻率圖如圖3.4所示,和相位延遲圖如圖3.5所示,其主要濾波器參數設置為:(1)響應類型為帶通;(2)設計方法為等波紋;(3)濾波階數為最小階數;(4)密度因素為20;(5)頻率參數中采樣頻率Fs=1000kHz,帶通頻率Fpass1=90kHz, Fpass2=140kHz,帶阻頻率Fstop1=80kHz,Fstop2=150kHz通帶紋波Apass=1dB,阻帶衰減Astop1=40dB,Astop2=40dB。
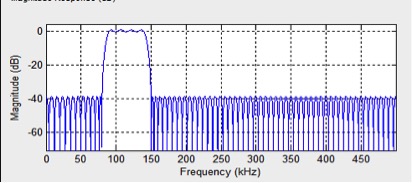
圖3.4 幅值—頻率圖

圖3.5 相位延遲圖
利用設計好的濾波器對采集到的鋼桶聲發射信號進行濾波,步驟如下:打開fdatool界面的file,選擇Export;輸出的變量名默認為Num,然后在編輯器里設置b=Num,a=1,x=filter(b,a,A);具體程序如圖3.6所示。經過濾波器濾波后得到鋼桶聲發射信號波形如圖3.7所示。

圖3.6 濾波程序部分代碼

圖3.7 濾波后聲發射信號時域波形
在時域中比較聲發射濾波前后如圖3.15和圖3.7,可見圖3.7中的低頻噪聲經過濾波器濾波后得到了弱化,這樣使得濾波后的時域信號波形比原信號的波形更加清晰可見,如圖可知,濾波后的信號中還存在一些低頻干擾,使濾波后時域信號出現高低不定的不規則脈沖。而且在對聲發射信號濾波的開始時還出現了小部分信號的失真,這失真主要是因為濾波器在進入完全工作前的延遲所致[4]。
3.1.3 功率譜估計
功率譜估計的目的是根據有限數據給出信號、隨機過程的頻率成分分布描述。對濾波后的鋼桶聲發射信號進行功率譜估計得到如圖3.9所示波形。具體程序如圖3.8所示:

圖3.8 功率譜估計部分程序代碼

圖3.9 聲發射信號功率譜密度
根據對多組采集到的鋼桶聲發射信號進行功率譜估計分析可知,聲發射功率譜密度幅值是隨鋼桶的泄漏孔徑增大而增大的,而標準鋼桶的聲發射信號的功率譜密度最大幅值在310-6左右。若鋼桶的聲發射信號的功率譜密度最大值的數量級超過了110-5則該鋼桶很可能為泄漏鋼桶。
3.1.4希爾伯特黃變換(HHT)
希爾伯特黃變換通過對聲發射信號局部特征分析,由信號本身的構造基函數分析,分解獲得不同大小的聲發射信號分量。本證模態函數代表了鋼桶聲發射信號的內在波動模式,對經驗模態分解后的固有模態函數分量進行分析可獲取信號中比較豐富的豐富的時頻能量信號,如圖10所示,對采集到的0.5mm孔徑泄漏狀態下的聲發射信號進行經驗模態分解,分解圖形如圖3.11所示,并對分解后的信號進行希爾伯特譜分析和邊際譜分析。

圖3.10 經驗模態分解部分程序代碼
從圖3.11中可以看出,經過經驗模態分解獲得了7個固有模態函數分量,經過對這幾個分量的具體分析可知,第1個固有模態函數分量為鋼桶泄漏聲發射信號中的特征頻率最大的分量,它對應的是頻率為110kHz左右的泄漏聲發射信號,而第2個固有模態函數分量對應的是頻率為25kHz的噪聲信號,而第7個固有模態函數分量則為鋼桶泄漏聲發射信號中的特征頻率最小的分量。

圖3.11 泄漏信號的經驗模態分解圖
我們對圖3.11中的泄漏信號經過經驗模態分解所得到的固有模態函數分量進行希爾伯特變換,可以得到的如圖3.12所示的希爾伯特譜和如圖3.13所示的邊際譜。在圖3.12中和圖3.13中有位于25kHz附近和位于110kHz附近的信號頻率,在根據前面分析的頻譜和功率譜可知,25kHz附近的信號為噪聲,而鋼桶泄漏聲發射信號的頻率位于110kHz附近。分別對不同大小孔徑的鋼桶聲發射信號做希爾伯特黃變換得出信號的能量變化,泄漏孔徑越大,邊際譜的能量就越大。

圖3.12 泄漏信號希爾伯特譜圖

圖3.13 泄漏信號邊際譜圖
分別對濾波后的多組標準鋼桶聲發射信號數據和不同泄露孔徑大小的鋼桶聲發射信號數據進行邊際譜分析比較,得出標準鋼桶聲發射信號的邊際譜最大值都低于1.3,若鋼桶的聲發射信號的邊際譜超過了1.3,則該鋼桶為泄漏鋼桶。
3.2 泄漏信號的時域分析
3.2.1 信號的時域仿真波形及其分布
從聲發射信號的時域波形上可以看到鋼桶泄漏信號的幅值特征隨鋼桶泄漏孔徑變化的變化隨時間變化情況的反映,因此,從時域仿真波形中可以看出幅值的變化。在鋼桶泄漏實際檢測過程中,由于鋼桶泄漏源聲發射信號很微弱,通常利用放大電路對采集到的微弱泄漏聲發射信號進行放大,轉化為一定大小的數字信號數據,然后再經輸入設備輸入計算機進行分析處理。如圖3.14所示,將標準信號、0.2mm孔徑泄漏信號、0.5mm孔徑泄漏信號、1.0mm孔徑泄漏信號的數據分別賦給A B C D,然后進行繪圖,橫坐標為時間,縱坐標為幅值,運行程序。運行結果如圖3.15所示。
如圖3.15所示,鋼桶泄漏聲發射信號的仿真時域波形上只能得到聲發射泄漏信號幅值的大概變化,而不能對信號進行詳細的描述和分析。因此要想獲得鋼桶泄漏聲發射信號的時域特征參數,我們還需要對聲發射信號做進一步的定量分析。

圖3.14 繪制時域波形程序

圖3.15 鋼桶聲發射信號時域波形
為了更好的分析鋼桶泄漏聲發射信號的時域特征參數的特點,將輸入到計算機的鋼桶泄漏聲發射信號分別按照標準鋼桶聲發射信號和泄漏鋼桶泄漏時孔徑大小不同的聲發射信號分成5組,分別對每一組信號的幅值進行統計,根據統計結果做出表格,由表格來分析信號幅值的特征。
表3.1 泄漏孔徑大小與幅值的關系
| 孔徑大小 |
0mm(標準) |
0.2mm |
0.3mm |
0.5mm |
1.0mm |
幅值大小v |
0.0012 |
0.0019 |
0.0067 |
0.025 |
0.14 |
由表3.1可以看出,在鋼桶內壓力大小相同時,泄漏的孔徑越大,聲發射信號的幅值就越大。

圖3.16 泄漏孔徑大小與幅值的關系
依次將表3.1的上的點的坐標連接起來,則可畫出標準鋼桶和不同泄漏孔徑鋼桶泄漏信號的幅值分布曲線,如圖3.16。從圖中可以看出鋼桶泄漏聲發射信號隨聲發射源特征不同而不同的幅值分布。其分布是有標準鋼桶和隨鋼桶桶泄漏孔大小的不同而不同的,當泄漏孔直徑較大時,鋼桶聲發射信號幅值較分散,它的正負幅值的最大差就越大,當鋼桶泄漏孔直徑較小或不泄露時,鋼桶聲發射信號的幅值則更集中,它的正負幅值的最大就越小。這說明泄漏信號的分布與泄漏孔徑有很大的關系。
3.2.2 聲發射時域信號的均值(SAL)及均方值(RMS)
對隨機信號時域特征參數的分析是有效描述隨機信號的方法,聲發射信號的時域特征參數主要有均方值、均值和方差等。分別對標準鋼桶、0.2mm、0.5mm、1.0mm孔徑大小的泄漏鋼桶做實驗,每組作五次,程序如圖3.17所示。如表3.2所示,分別求出幾組濾波后鋼桶聲發射信號的均方值和均值。

圖3.17 求均值均方值部分程序
表3.2 泄漏信號時域特征量計算結果
| 孔徑 |
特征量 |
第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
標準(0mm) |
均值 |
-8.5027e-07 |
-6.79274e-07 |
-5.70537e-07 |
-9.55546e-07 |
-8.18635e-07 |
均方值 |
0.00017607 |
0.000206035 |
0.000160567 |
0.000169151 |
0.000164451 |
0.2mm |
均值 |
-1.0008e-06 |
-9.33033e-07 |
-9.51477e-08 |
-8.98199e-07 |
-6.04869e-07 |
均方值 |
0.00037687 |
0.000381093 |
0.00035149 |
0.000352732 |
0.000373246 |
0.5mm |
均值 |
5.9555e-08 |
2.53018e-06 |
-2.5355e-06 |
5.61606e-07 |
-5.76241e-06 |
均方值 |
0.00511135 |
0.00518833 |
0.00524539 |
0.00611025 |
0.00552995 |
1.0mm |
均值 |
-1.2324e-05 |
1.15988e-06 |
4.02003e-06 |
-1.02038e05 |
4.22021e-06 |
均方值 |
0.0106125 |
0.0118906 |
0.0118194 |
0.00949618 |
0.0111874 |
從表3.2中可知,均值的不能顯示出鋼桶泄漏源的特征。而對于均方值,在相同泄漏孔徑大小的鋼桶泄漏信號的均方值每次測試的結果變化不大;而不同孔徑的鋼桶的均值是隨著孔徑的變大而變大。由此可見,在工程中可以由均方值的大小來判斷泄漏孔的大小。
3.3本章小結
本章詳細敘述了泄漏信號的特點及處理方法,分別對泄漏信號的時域和頻域進行研究,重點對泄漏信號的時域均方值、快速傅里葉變換、功率譜、希爾伯特黃變換進行了實驗研究和分析。運行自己開發的鋼桶泄漏聲發射信號檢測系統對鋼桶聲發射信號進行分析處理,得出濾波后鋼桶泄漏信號的分析結果如下表所示:
表3.3 不同泄漏孔徑的信號特征參數
| 泄漏孔徑大小 |
均方值(RMS) |
FFT最大幅值 |
功率譜最大幅值 |
邊際譜最大幅值 |
標準(0mm) |
0.000176075 |
0.00010011 |
5.1312e-06 |
9.6792e-09 |
0.2mm |
0.000386193 |
0.00021886 |
2.4524e-05 |
2.24584e-08 |
0.5mm |
0.00511135 |
0.0031134 |
0.004963 |
4.8933e-07 |
1.0mm |
0.0106125 |
0.0055116 |
0.015553 |
8.8119e-07 |
根據表3.3得出,泄漏聲發射信號的頻域特征參數和均方值是隨鋼桶泄漏孔徑的增大而增大。
[1] 姜濤.管道泄漏檢測與定位的應用研究[D].哈爾濱工程大學,2008.
[2] 楊麗娟,張白樺,葉旭楨.快速傅里葉變換FFT及其應用[J].光電工程,2004,31(增刊):1-7.
[3] 胡麗瑩,肖蓬.快速傅里葉變換在頻譜分析中的應用[J].福建師范大學學報(自然科學版), 2011(04).
[4] 宋愛國,劉文波等.測試信號分析與處理[M].機械工業出版社,2007.
[5] 黃振峰,伍蔣軍,毛漢領.金屬裂紋聲發射信號FIR濾波設計的濾波器參數設置方法[J].河北工業大學學報,2007(01):36.
[6] 于浩.石油管線泄漏的聲發射技術(AE)監測系統研究[D].西安科技大學,2009.
【相關鏈接】
基于時頻域的鋼桶泄漏檢測信號處理(1)
基于時頻域的鋼桶泄漏檢測信號處理(2)
基于時頻域的鋼桶泄漏檢測信號處理(3)
基于時頻域的鋼桶泄漏檢測信號處理(4)
基于時頻域的鋼桶泄漏檢測信號處理(5)
|

