《包裝設計制作工藝與檢測技術標準實用手冊》

第四篇　包裝設計基礎

第三章　包裝容器結構設計

第一節　紙包裝容器結構設計

2．管式折疊紙盒的旋轉性、成型角和旋轉角

（1）旋轉性。管式折疊紙盒盒體的成型過程，可以看成是與盒底面截交的各個側面，以相鄰兩側面的相交線為軸，依次旋轉一定角度而成型。見圖4－3－22，正四棱柱紙盒和正六棱柱紙盒，其側面B′BCC′面、C′CDD′面……分別以BB′、CC′……為軸依次旋轉90°和60°而成型。管式折疊紙盒這種連續旋轉成型特性即為管式折疊紙盒的旋轉性。

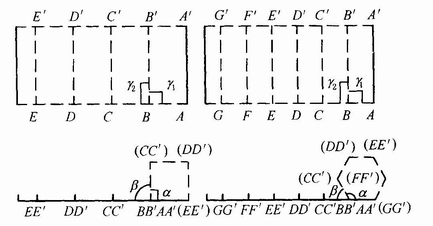
圖4－3－22　管式折疊紙盒的旋轉性

（2）成型角

A成型角　如圖4－3－22所示，在成型時，相鄰兩側的底邊（或頂邊）所構成的角，稱為第一類成型角，簡稱A成型角，用α表示。

B成型角　在各個側面中，底邊（或頂邊）與旋轉軸（相鄰兩側面的交線）所構成的角稱為第二類成型角，簡稱B成型角，用γi表示（圖4－3－22）。

（3）旋轉角。在成型中，相鄰兩側面的底邊或頂邊以其交點為軸，所旋轉的角即為旋轉角，用β表示（見圖4－3－22）。在實際上，管式折疊紙盒盒底（或盒蓋）在成型過程中，相鄰兩側面的搖翼為構成A成型角而旋轉的角度即等于β。

由于管式折疊紙盒是由一平面紙板折疊而成，故就同一旋轉點來說，A、B類成型角和旋轉角之間存在如下關系：

β＝360°－（α＋Σγi）　　　　（4－3－4）

式中　β———旋轉角，（°）；　α———A成型角，（°）；∑γi———B成型角之和，（°）。

3．管式折疊紙盒的盒蓋結構

對于紙盒盒蓋的結構設計，首先應考慮便于被包裝物的裝入和取出，在被包裝物裝入后不會自開，起到保護被包裝物的作用；其次盒蓋應能易開和易封。

在盒蓋的設計中，可采用以下幾種方法固定盒蓋，防止自開。

a．利用紙板間的摩擦作用，固定盒蓋。

b．利用紙板上的卡口，卡住搖翼，固定盒蓋。

c．利用插口插舌結構，將搖翼互相鎖合，固定盒蓋。

d．利用搖翼互相插撇鎖合，固定盒蓋。

e．利用粘合劑將搖翼粘合，固定盒蓋。

管式折疊紙盒盒蓋的種類很多，有具有多次開啟功能的；有防偽和防盜功能，只能開啟一次，不能復原的；有雖然只能開啟一次，但在取出被包裝物后可以在新的位置做新蓋的；還有在開啟后可以兼做廣告板的。

盒蓋的結構形式按盒蓋固定方式的不同主要有如下幾種。

（1）插入式。見圖4－3－23，插入式盒蓋在盒的端部設有3個搖翼，主搖翼適當延長，封蓋時插入盒體。此種盒蓋具有再封合功能，可多次使用。插入式盒蓋有飛機式、反插式和直插式3種。

（2）鎖口式。鎖口式盒蓋一般有4個搖翼，在相對的兩個主搖翼上設計有相應的插口和插舌，見圖4－3－24。這種結構是利用主搖翼上的插舌插入相應搖翼的插口內，固定盒蓋。其特點是封合牢固，但開啟稍嫌不便。

（3）插鎖式。插鎖式盒蓋是插入式和鎖口式相結合的一種盒蓋結構。常見的兩種結構見圖4－3－25。

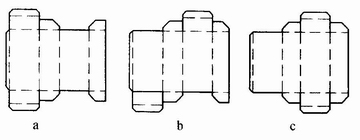
圖4－3－23　插入折疊紙盒

a．飛機式；b．反插式；c．直插式

（4）連續搖翼窩進式。這是一種特殊的鎖口形式，主要用于正多邊形管式折疊紙盒的盒蓋（或盒底）結構，見圖4－3－26。其特點是封口比較牢固，可通過折疊組成造型優美的圖案，但手工組裝比較麻煩。一般用作禮品包裝。

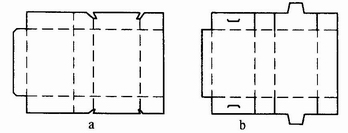
圖4－3－24　鎖口式折疊紙盒

圖4－3－25　插鎖式折疊紙盒

圖4－3－26　正n方棱連續搖翼窩進式盒蓋

連續搖翼窩進式盒蓋的設計要點是尋找各搖翼折插后的相交點O。對該點的要求是它必須位于各搖翼的輪廓邊線上或折痕線上，否則搖翼就無法折插并相互鎖合。而對搖翼的形狀，既可用簡單明快的直線，也可采用復雜多變的曲線。

各搖翼相交點的確定主要有以下兩種情況：

①正n邊形。對于正n邊形連續搖翼窩進式紙盒盒蓋搖翼的相交點，在設計中一般選擇其幾何中心。見圖4－3－27，正四邊形盒蓋的相交點位于其幾何中心，也位于A成型角（∠BAD）的角平分線AO與頂邊AB的中垂線OH的交點上。

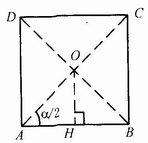
圖4－3－27　正四邊形盒蓋成型圖

對于正n邊形，其A成型角計算公式為：

α＝［180°×（n－2）］／n　　　　（4－3－5a）

故：

α／2＝［180°×（n－2）］／2n　　　　（4－3－5b）

式中　α———A成型角，（°）；　n———正n邊形的邊數。

由以上分析可知，正n邊形各搖翼相交點的確定方法為：通過搖翼側面頂邊的一個旋轉點，作與頂邊成α／2的射線和該頂邊中垂線的交點，即確定了該搖翼相交點的位置。其它搖翼用與此相同的方法確定。

該方法同樣適用于正n棱柱和正n棱臺管式折疊紙盒盒蓋的搖翼設計。

②任意n邊形。確定任意n邊形連續搖翼窩進式紙盒盒蓋搖翼相交點的方法較多，有展開法、垂足法和旋轉角法等。見圖4－3－28，在此以任意三邊形為例介紹展開法求解盒蓋搖翼的相交點。

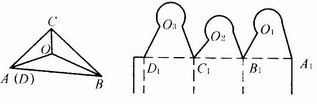
圖4－3－28　任意三邊形相交點的求法

求解盒蓋各搖翼相交點Oi的步驟如下：

第一步，選取盒蓋上的任意相交點O（見圖4－3－28a），連接相交點O與旋轉點的連線OA、OB、OC；

第二步，將三角形ABC依次展開成線段A1B1C1D1；

第三步，在線段A1B1上以A1點為圓心，以OA為半徑作一圓弧，然后再以B1點為圓心，以OB為半徑再作一圓弧，兩圓弧相交點O1就是A1B1側面搖翼上的相交點；

第四步，按第三步相同的方法求取B1C1，C1D1側面搖翼上的相交點O2和O3。

以此類推對任意正n邊形，均可采用上述展開法求取各搖翼上的相交點Oi。此外展開法還可用于求盒蓋上各搖翼的重合點，以便在盒蓋上打孔來安裝緞帶等物。

其它確定連續搖翼窩進式紙盒盒蓋搖翼相交點的方法，由于篇幅所限在此不再贅述。

返回目錄頁