《包裝設計制作工藝與檢測技術標準實用手冊》

第四篇　包裝設計基礎

第三章　包裝容器結構設計

第一節　紙包裝容器結構設計

3．盤式折疊紙盒的盒蓋結構

（1）罩蓋式。其盒蓋盒體是兩個獨立的盤式結構，盒蓋的長度和寬度尺寸一般比盒體略大些。這種紙盒多用于高度較小而盒面積較大的商品，便于展示裝潢設計。

按照盒體盒蓋的相對高度，罩蓋盒可分為3種結構類型。

①天罩地式　H′1≥H1（圖4－3－45a），盒蓋完全罩住盒體。

②帽蓋式　H′1＜H1（圖4－3－45b），盒蓋只罩住盒口部分。

③對口蓋式　H＝H′1＋H1（圖4－3－45c），盒蓋罩住盒口的插口部分。

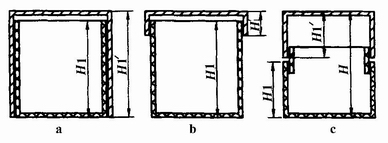
圖4－3－45　罩蓋盒的結構類型

對于罩蓋盒，其有關尺寸計算公式為：

盒體　　　X＝Xi＋（m＋1）t＋kX　　　　（4－3－10）

　　　　　X0＝X＋t＝Xi＋nt＋kX　　　　（4－3－11）

盒蓋　　　X′＝X0＋（m－1）t＋kX′＝Xi＋（m＋n－1）t＋kX＋kX′　　　　（4－3－12）

　　　　　X′0＝X1＋（m＋n）t＋kX＋kX′　　　　（4－3－13）

式中　Xi———盒體內部尺寸，mm；　X———盒體制造尺寸，mm；　X0———盒體外部尺寸，mm；　X′———盒蓋制造尺寸，mm；　X′0———盒蓋外部尺寸，mm；　n———盒體紙板層數；　m———盒蓋紙板層數；　t———紙板厚度，mm；　kX———盒體制造尺寸修正函數，mm；　kX′———盒蓋制造尺寸修正系數，mm。

（2）搖蓋式。盤式搖蓋盒是在盤式盒的基礎上加以鉸鏈式搖蓋組成全封口結構的盤式盒。此類盤式紙盒有單搖蓋和雙搖蓋兩種，見圖4－3－46。

圖4－3－46　盤式搖蓋紙盒
a．單搖蓋紙盒；b．雙搖蓋紙盒

（3）插別式。此類盤式折疊紙盒類似于連續搖翼窩進式盒蓋，見圖4－3－47。

圖4－3－47　插別式盤式折疊紙盒

（4）正掀封口式。正掀封口式盤式折疊紙盒的盒蓋與管式折疊紙盒中的正掀封口式盒蓋相同，見圖4－3－48。

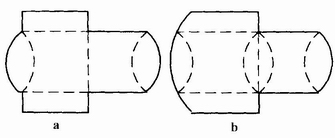
圖4－3－48　正掀封口式盤式折疊紙盒

4．盤式自動折疊紙盒的結構設計

（1）盤式自動折疊紙盒。盤式自動折疊紙盒成型后，可將兩端側板折向盒內，而將整個紙盒折成平板狀，使用時，只要張開盒身，紙盒就能自動恢復成型。

根據其折向有內折疊盤式紙盒和外折疊盤式紙盒，即紙盒左右的側板折向盒內時，其前后側板向外翻折時為外折疊盤式紙盒；而當紙盒的左右側板折向盒內時，前后側板也折向盒內的為內折疊紙盒，見圖4－3－49。

最典型的盤式自動折疊紙盒是畢爾斯（Beers）式折疊紙盒和布萊特伍茲（Bright－woods）式折疊紙盒。它們最大的特點是γi＝90°。這兩種盤式自動折疊紙盒結構見圖4－3－50，均有內折疊式和外折疊式兩種，結構樣式大同小異。

圖4－3－49　盤式自動折疊紙盒折成平板狀圖
a．外折疊紙盒；b．內折疊紙盒

圖4－3－50　畢爾斯式和布萊特伍茲式自動折疊紙盒
a．畢爾斯式；b．布萊特伍茲式

（2）內折疊角。設計盤式自動折疊紙盒時，一般先要計算其內折疊角的大小。內折疊角的含義為：為使棱臺形盤式自動折疊紙盒在成型后，其兩側的側板能向盒內平折，在側板上形成的折疊線與紙盒底邊構成的角見圖4－3－51中的∠C1OO3（或∠COO3）。

內折疊角的一般計算公式為：

θ＝12（α＋γ1－γ2）　　　　（4－3－14）

式中　θ———盤式自動折疊紙盒的內折疊角，（°）；　α———A成型角，（°）；　γ1———內折疊角所在盒板即側板的B成型角，（°）；　γ2———與γ1所在盒板即端板的B成型角，（°）。

（3）外折疊角。外折疊角的含義為：為使棱臺形盤式自動折疊紙盒成型以后其兩側側板能向盒外平折，在側板上形成的折疊線與紙盒底邊所構成的角，見圖4－3－52中的∠COO3，用θ′表示。

外折疊角的一般計算公式為：

θ′＝（γ1＋γ2－α）／2　　　　（4－3－15）

式中　θ′———盤式自動折疊紙盒的外折疊角，（°）；　α———A成型角，（°）；　γ1———外折疊角所在盒板的B成型角，（°）；　γ2———與γ1相鄰盒板即邊板的B成型角，（°）。

對于前述的畢爾斯式和布萊特伍茲式盤式折疊紙盒，由于其α＝γ1＝γ2＝90°，此類紙盒的內折疊角和外折疊角相等均勻45°。

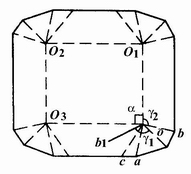
圖4－3－51　盤式自動折疊紙盒內折疊角

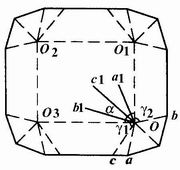
圖4－3－52　盤式自動折疊紙盒外折疊角

返回目錄頁